[Error rate calculation] quick calculation for PCR and sequencing errors

Summary

Improved
Q5 for PCR: 8.4*10^-4
Paired-end sequencing: 6.9*10^-5

Previous
Taq for PCR: 0.162
Single read sequencing: 5.2*10^-2

---------Explanations-----------------
PCR error rate:
Q5: https://www.neb.com/products/m0491-q5-high-fidelity-dna-polymerase
~280 lower than Taq

 https://www.neb.com/tools-and-resources/feature-articles/polymerase-fidelity-what-is-it-and-what-does-it-mean-for-your-pcr


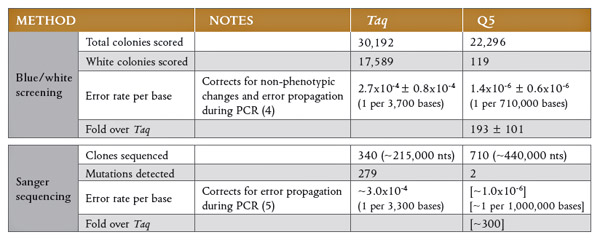
PCR_Q5 = 1.4*10^-6
PCR_Taq =2.7*10^-4

After 30 cycles of PCR amplification for 20bp barcode,
The probability for one of the sites being mutated is
Q5: 1.4*10^-6*20*30 = 0.00084 = 8.4*10^-4
Taq: 2.7*10^-4*20*30 = 0.162

Sequencing error rate：
The HiSeq data sets showed the lowest substitution rates of all three platforms with average rates of 0.0026 (errors per base) for R1 and 0.0040 (errors per base) for R2.

For single read
Error rate = 0.0026*20 = 5.2*10^-2

For paired-end seq, if we threw away reads when there is a base that is inconsistent.
Error occurs only when the base is mutated into the same wrong base
Error rate = 0.0026/3*0.0040/3*3*20 =6.9*10^-5

So by using Q5 and paired-end sequencing, the error rate is still restricted by Q5.
Reducing the number of PCR cycles may help, but not much (linearly), but the product is decreasing exponentially. May reduce a few cycles because over-amplification is not very accurate and may cause additional problems.
If we use 15 cycles
Q5: 1.4*10^-6*20*15 = 0.00042 = 4.2*10^-4

If Q5 doesn't work, Kapa Hifi is another option that works with similar (slightly lower) accuracy.

Reference: Bronner et al, 2009, Improved Protocols for Illumina Sequencing



Comments

  1. ChrisSeptember 25, 2017 at 11:28 PM

    FYI, with paired-end sequencing of Q5 DNA polymerase, we observed error rates of 1.4 x 10^-3 per 20 bp sequence --just about what should be expected from your calculations.

    So it seems like you're right: PCR fidelity still limits the error rate even with Q5. If we want to improve the error rate further, we'd need to reduce the PCR cycles.

    Thanks!

    ReplyDelete
  2. Dmitri PetrovSeptember 30, 2017 at 8:54 AM

    I am actually very happy with this. It looks like the two error rates are about the same meaning that we are no wasting effort in either place.

    ReplyDelete

Post a Comment

Popular posts from this blog

Quick notes about PCR amplification for Barcode sequencing

Image
Feel free to share the blog and discuss^_^ Several guidelines Guideline for a general reference： 2014-Measuring the activity of protein variants on a large scale using deep mutational scanning Having too many PCR amplification cycles may not be very good, because 1) Error increases linearly with the number of cycles under usual conditions, (but the product would increase exponentially). 2) Over amplification towards the end of PCR may have reduced accuracy. About the bubble product Overamplification of PCR may cause bubble product to form, resulting in higher error rate but won't cause problems for sequencing (such as clustering, because denatured libraries have complete adapters on either side for sequence). Figure 1. Illumina bubble product example For actual amplicon sequencing, the secondary peak will be closer due to smaller bubbles. Figure 2. My previous amplicon sequencing bubble product. The left and right ones are the lower and upper...
Read more

Sequencing primer design for barcode sequencing

Image
General rules and other notes: 1. Why do we need to add random N for the forward primer 5-7 cycles for R1 is used for both R1 and R2 to locate the cluster and color matrix during sequencing. May need to use less dense clusters. Transitions from high to low diversity sometimes matter for getting a high sequence quality, as told by an Illumina scientist. 2. Spike-in guideline The newer software allows us to forgo costly control lanes but instead use extra phiX. For amplicons, at least 5-10% is needed to overcome low diversity issue 3. About random Ns/degenerate oligos/mixed base; (iDT Note) When mixed bases are used, the oligo is a mixture of the bases in certain positions. There are two ways of having random Ns, machine mix and hand mix. machine mix: T is up to 30% Hand mix: is about 24% The length limitations for hand mix oligos is and was 100nt. Machine mix will only do 25% each. Machine mix tends to over-represent G slightly and under-represent A. ...
Read more